Address
12 Rue de Cléry, 75002 Paris
Work Hours
Jeudi et Vendredi: de 9H à 18H
Mathématique
CHAPITRE I: Nombre binaire
Binaire
Un système binaire est un système de numération en base 2. Le système le plus répandu est celui n’utilisant que des 0 et des 1, grâce à la notation positionnelle, c’est-à-dire que la position d’un chiffre est reliée à la position voisine par un multiplicateur : 10 dans le système décimal et donc 2 dans le système binaire. Chaque chiffre équivaut à un bit, qui vient du terme anglais binary digit, « caractère binaire » en français.
Si des systèmes binaires ont été utilisés dès l’Antiquité, en Chine et en Inde notamment, l’invention du système binaire actuel est attribué au mathématicien allemand Gottfried Wilhelm Leibniz à la fin du XVIIe siècle. Aujourd’hui, le système binaire est essentiellement utilisé comme langage de bas niveau en informatique.
Décimal
Un nombre décimal est un nombre réel qui peut s’écrire exactement avec un nombre fini après la virgule. 34 est la partie entière, et 68 est la partie décimale. Les décimales, ce sont tous les chiffres après la virgule.
Hexadécimal
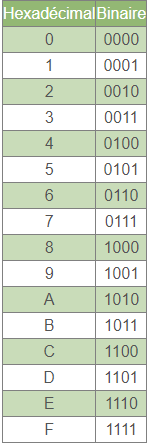
A la différance des deux autre l’hexadécimal peut comporter des lettres le tableau si dessous montre sont lien avec le binaire
Conversion Binaire->Décimal
Pour chaque 1 dans le nombre binaire dois être multiplier par 2 puissance sa position et faire la somme des résultats obtenu
Conversion Binaire->Hexadécimal
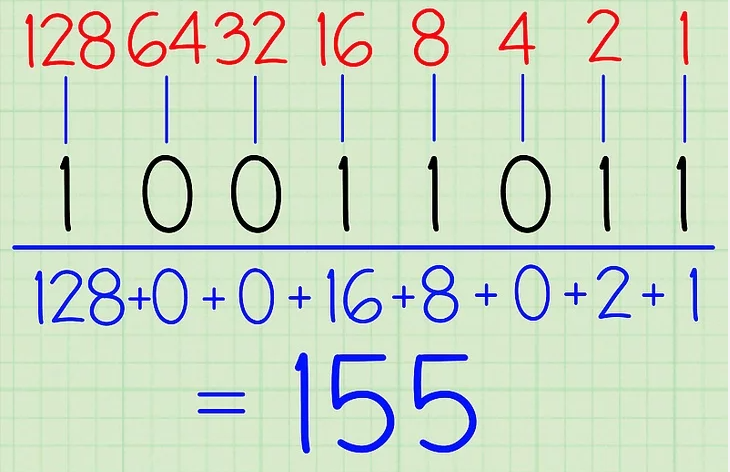
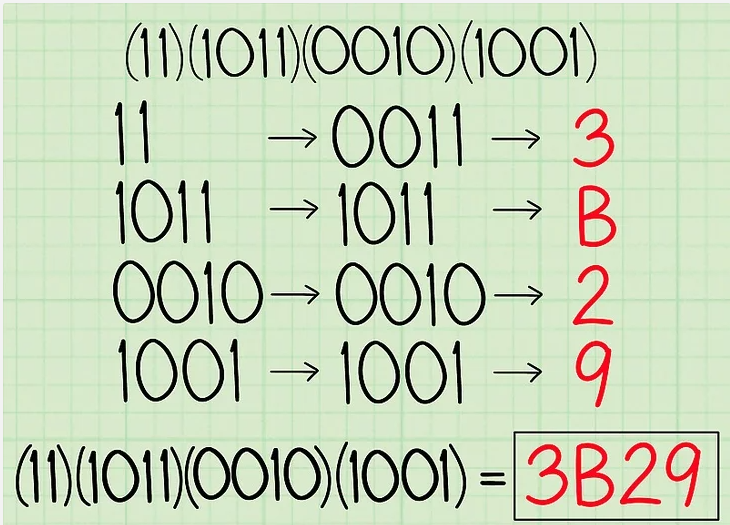
Il suffit de regarder le tableau Hexadécimal
Conversion Décimal->Binaire
diviser par 2 le nombre décimal, garder 1 lorsqu’il y a un reste et récupéré le binaire de bas en haut
Conversion Décimal->Hexadécimal
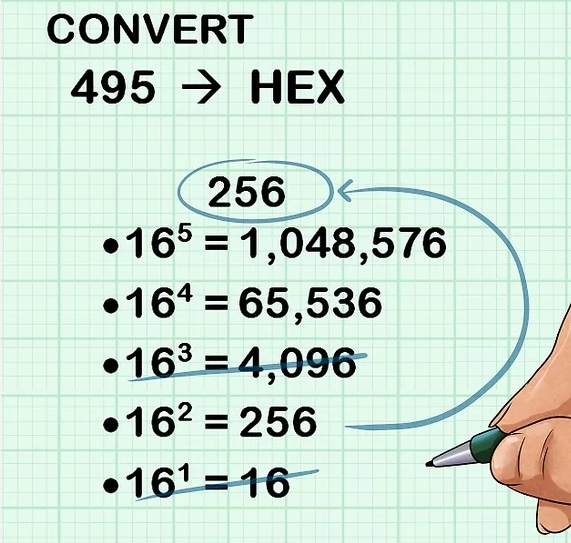
Etape1: Trouver le nombre le plus proche du décimal dans un tableau 16 puissance position décimal>= tableau 16 puissance position
Etape2: décimal/tableau 16=quotient1 prendre le nombre avant la virgule
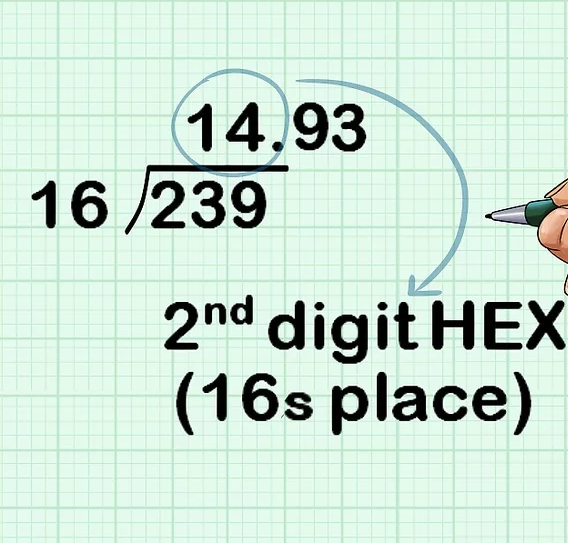
Etape3: quotient1 x tableau 16 =produit1 ensuite décimal-produit1=différence1
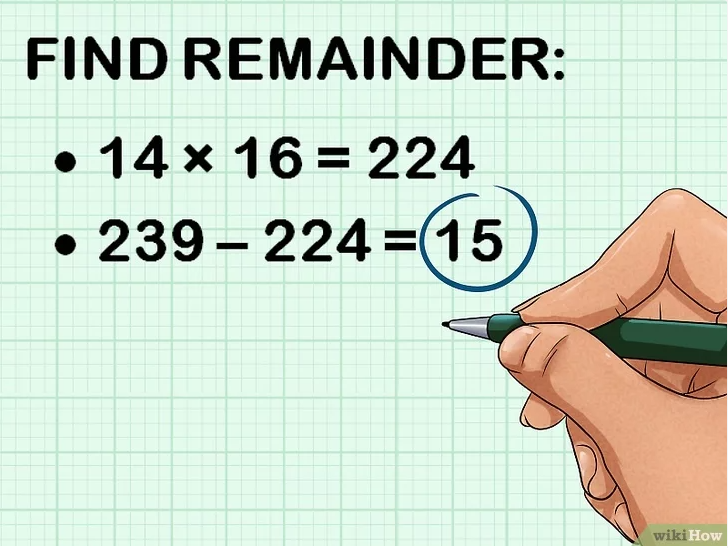
Etape4: différence1/16=quotient2 prendre le nombre avant la virgule
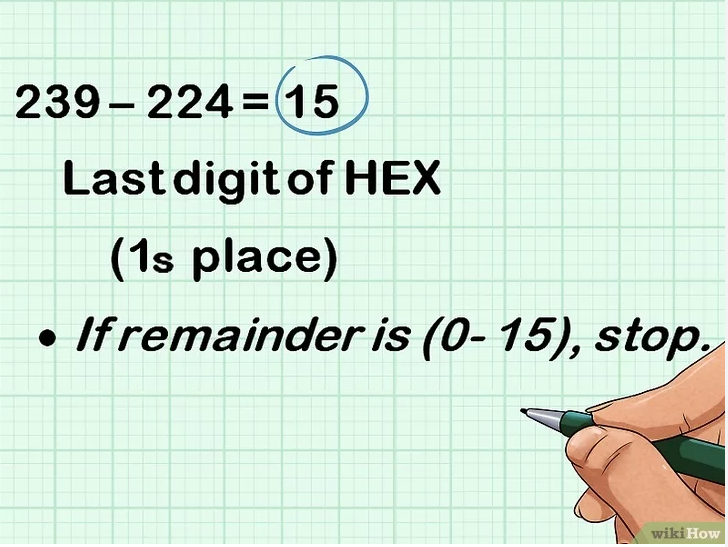
Etape5: quotient2 x 16 =produit2 si le résulta est égal ou inferieur a 15 la boucle se ferme
Etape6: voir les résultats entre la grille décimal et hexadécimal
Conversion Hexadécimal->Binaire
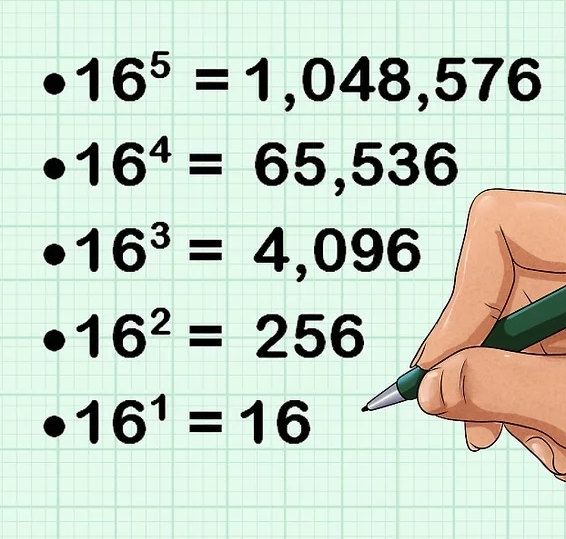
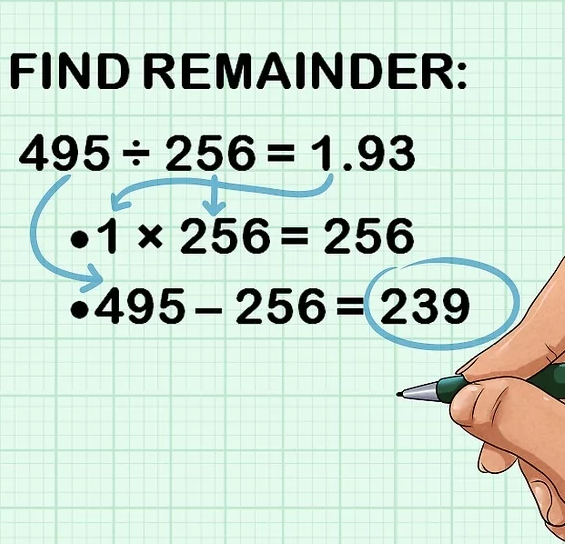
Comparer les deux grille
Conversion Hexadécimal->Décimal
Multiplier les nombre avec 16 puissance position
CHAPITRE II: Algèbre de Boole
Explication
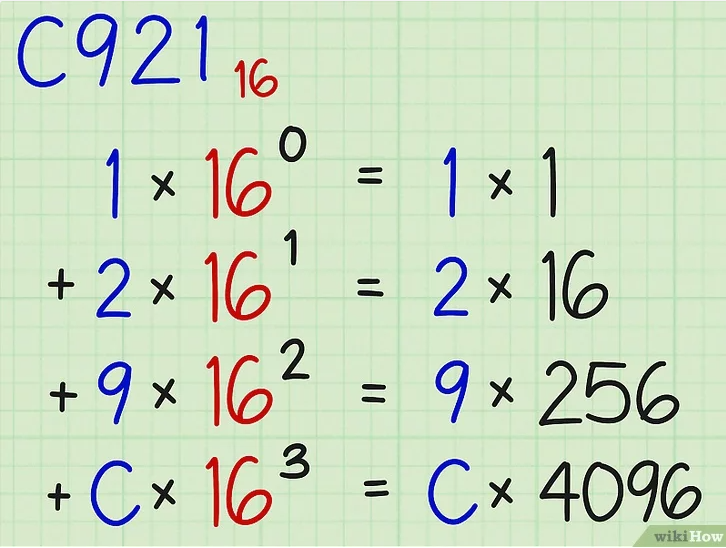
L’algèbre de Boole, ou calcul booléen, est la partie des mathématiques qui s’intéresse à une approche algébrique de la logique, vue en termes de variables, d’opérateurs et de fonctions sur les variables logiques, ce qui permet d’utiliser des techniques algébriques pour traiter les expressions à deux valeurs du calcul des propositions. Elle fut lancée en 1854 par le mathématicien britannique George Boole. Aujourd’hui, l’algèbre de Boole trouve de nombreuses applications en informatique et dans la conception des circuits électroniques.
L’algèbre de Boole des fonctions logiques permet de modéliser des raisonnements logiques, en exprimant un « état » en fonction de conditions. Par exemple, si nous étudions l’expression Communication et l’expression Décrocher.
Example:
On définit les variables booléennes a, b et c de la façon suivante :
- le commentaire a eu strictement mois de 100 vues et est daté de strictement mois de 6 mois,
- ou le commentaire a été écrit par un anonyme et a eu 100 vues ou plus,
- ou le commentaire est daté de 6 mois ou plus et a eu 100 vues ou plus,
- ou le commentaire est daté de strictement moins de 6 mois et n’a pas un anonyme.
On définit les variables booléennes a, b et c de la façon suivante :
- a=1 si le commentaire a strictement mois de 6 mois : -a=0 sinon ;
- b=1 si le commentaire comptabilise strictement mois de 100 vues : -b=0 sinon ;
- c=1 si l’auteur du commentaire est anonyme : -c=0 sinon ;
Si l’on fait l’ensemble des demande cela donne: E=ab+(-bc)+(-a-b)+(a-c)
Le diagramme de E correspond a:
Pour simplifier il suffit de regrouper les zones collé les groupe se font de 2 et de 4:
- 2 est égale a deux valeur
- 4 est égal a une valeur
la version simplifier serai donc E=a-b et son contraire est si on en croit le diagramme et le Morgan serai -E=-ab
Exercice: Algèbre de Boole
Partie A :
| Sommets | Heures | Prédécéseurs | Succeseurs | Niveaux |
| A | 2 | C,E | 0 | |
| B | 3 | E | 0 | |
| C | 6 | A | D | 1 |
| D | 7 | C,E | G | 2 |
| E | 4 | A,B | D,F | 1 |
| F | 6 | E | G | 2 |
| G | 2 | D,E | H | 3 |
| H | 1 | G | | 4 |
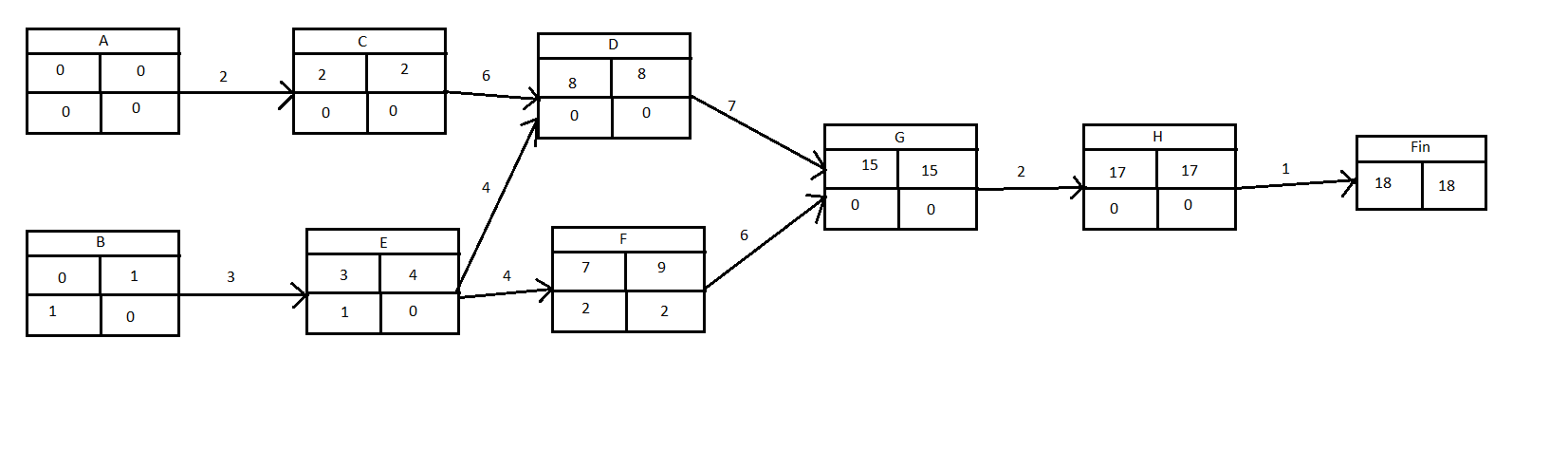
Partie B :
Le matériel vidéo est acheté dans un magasin local et est de fabrication française
Le matériel vidéo n’est pas de fabrication française et il coûte moins de 500 euros;
Le matériel vidéo n’a pas été acheté dans un magasin local, est de fabrication française et a coûté moins de 500 euros.
a le matériel vidéo coûte moins de 500 euros et a le matériel vidéo coute 500 euros ou plus
b le matériel vidéo est acheté dans un magasin local et b le matériel vidéo n’est pas acheté dans un magasin local.
c le matériel vidéo est de fabrication française et c le matériel vidéo n’est pas de fabrication française.
E=bc+aĉ+aƀc
E=a+bc
Dans le projet présenté, le matériel vidéo coûte plus de 500 euros, n’est pas de fabrication française mais sera acheté localement.
| a=0 | E=0+1*0 | |
| ā=1 | E=0 | Le projet est rejeté |
| c=0 | ||
| ĉ=1 | ||
| b=1 | ||
| ƀ=0 |